In my 12th year of teaching, I continue to be amazed at the misconceptions surrounding multi-digit subtraction. In my experience, students who are masters at memorizing the steps of the US standard algorithm are quite successful, though have little understanding of the place value. Why do we borrow? What does that even mean?
In an effort to do a much better job this year, I am trying a new strategy. Given the problem:
634 – 368 = z
I am requiring my students to write out each number in expanded form:
634 = 600 + 30 + 4
368 = 300 + 60 + 8
The language that I am using with this strategy is intentional. Since we cannot take 8 from 4, we need to borrow a ten, thus changing the 30 to a 20 and changing the 4 to a 14. I am stressing with students that this is the same value:
600 + 30 + 4 = 600 + 20 + 14
This alone is mind-blowing!
So now, if we finish the problem, it looks like:
The power in this language is that now, rather than saying: “What is 12 – 6? ” I am now saying, “What is 120-60?” My hope is that by changing the way I speak, I am deepening students’ understanding of place value, and how we talk about it. The best part of this is that when I revert to my old ways (which I do), students immediately correct me by saying, “Excuse me, Mrs. Nied, but that is not 12-6–it is 120-60.” Students have completely taken over this language and I am hearing it constantly in group discussions. Woo hoo!
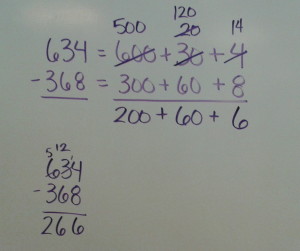
This is a great example of what Common Core means to me: we slow down and look closer at what we do when we go through the motions of math. Without these “aha” moments, some kids will forever be confused when we say “carry the one!” or “borrow from the 5”. But with this groundwork, even though it may seem boring or obvious to others, those other kids won’t get left in the dust.
This is awesome. It reminds me of what my sixth graders did instead of borrow as soon as they learned about the wonderful world of numbers to the left of zero. Stay tuned for my next post.
I was talking with a 4th grade teacher at my school today and she said they are all in love with math again. This is math with understanding – numeracy (like literacy) requires understanding.
Although I have been using the vocabulary you described for years, I have not written the problems out in expanded form – I love this! I am excited to try this with the two or three students I have who are still struggling with regrouping! Thanks for the great idea!