Educational Portfolio for Spencer Olmsted
Contact Information
Spencer Olmsted513 Central St NE
Olympia, WA 98506
(solmsted at yahoo)
2009-Current: 5th grade math and science teacher at Pioneer Elementary School in Olympia, Washington.
2006-2009: 5th grade teacher at L.P. Brown in Olympia.
Fall 2005: student taught in the 4th grade at Morning Star Elementary School in Bozeman, Montana.
Education
Links place content further down the page.Blog Entries
Graduate Work

Field trip to the Tinsley House at the Museum of the Rockies
Teaching Mathematics
The name for this site came to me as I thought about teaching and remediating fundamental mathematical models and principles.
Teaching math is an area of passion for me. I love showing children how to see patterns in numbers and helping them open the doorway for a personal connection to mathematics. The language of numbers is often misunderstood on a very basic level, but this does not have to be the case. While teachers of math must have a true understanding of the concepts involved, children need to be taught by someone who has a love of math. This love breeds a level of comfort and confidence that will help students navigate new areas in math with a playful attitude.
Through my graduate work at The Evergreen State College I have come to some very important realizations concerning the teaching of mathematics. My thesis on High-Press Questioning and Student Discourse is available to read, but here are some of the ideas with which I worked.
I wondered how student discourse would impact learning. I created an environment where students often worked in small groups on complex problems that may have had more than one solution and many possible ways to get there. Instead of answering questions that would reduce the thinking of the group, I asked questions of my own. Many students began the year asking for "help", but without having a specific question. I taught them to ask questions, and in doing so many of them found the answers themselves. If not, I was there to provide them with the next question they needed to ask. In this way I could provide the least help possible, so that the actual construction of new knowledge could take place in their brains.
A few concepts to work with...
Place Value
Understanding our number system in terms of bases, or place value.
| base-n | nx... | n3 | n2 | n1 | n0 |
| base-10 | 10x... | 103 | 102 | 101 | 100 |
| base-16 | 16x... | 163 | 162 | 161 | 160 |
Sequences and Patterns in Numbers
One of my favorite mathematical activities is examining patterns and figuring out equations that describe them. Patterns are so central to mathematics that some describe the field as a science of pattern and order. Recursive and explicit notation describe change over time. Let's examine a simple pattern.
| X | 1 | 2 | 3 | 4 | 5 | x |
| Y | 5 | 7 | 10 | 14 | 19 | f(x) |
One way to look at this pattern is that it grows at a faster rate as x increases. This means that this function does not describe a line. But what kind of curve? As we examine the first difference (FD) we notice that the rate of change is linear. The second difference (SD) shows that the rate of change is constant. Algebraically, we might note that this is the characteristic of 2nd degree polynomials (quadratic functions).
| X | 1 | 2 | 3 | 4 | 5 | x |
| Y | 5 | 7 | 10 | 14 | 19 | f(x) |
| FD | 2 | 3 | 4 | 5 | ... | |
| SD | 1 | 1 | 1 | 1 |
We might then compare our output to the parent function x2 to see if we can perceive the composition. We might also look at the function graphically to see how it has been transformed.
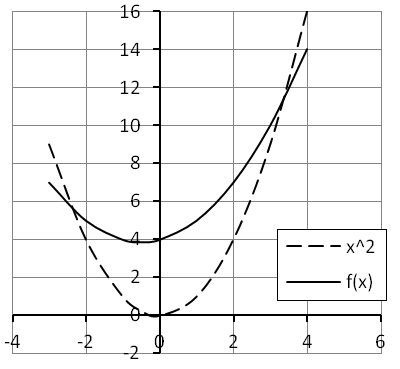
Here we can see that the function has been shifted up by 4 and slightly to the left. It has also been vertically compressed, which means that the leading coefficient is a fraction. And still there are many other ways to examine this pattern!
Prime Numbers
Beyond being a sequence of numbers, prime numbers form the building blocks of numbers.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37...
All numbers can be expressed as a product of prime numbers in one and only one way.
16 = 24
24 = 23 x 3
29 = 29 x 1 (prime)
Why is the number one not prime? (external)
Just for Fun
A monk begins walking from the bottom of the mountain at sunrise taking breaks for rest, food, and water as needed. He arrives at the monastary at the top of the mountain at sunset. The next morning he leaves the monastary at sunrise heading back down the mountain. Again he takes breaks as needed, but because of the downhill travel arrives at the bottom an hour before sunset. Prove that at one point the monk was at the same place on the mountain at the same time both days.